Review 26: A control-theoretic approach to brain-computer interface design

A control-theoretic approach to brain-computer interface design by Yin Zhang and Steven Chase

Zhang, Yin, and Steven M. Chase. “A control-theoretic approach to brain-computer interface design.” 2016 American Control Conference (ACC). IEEE, 2016.

  • A challenge in brain computer interface (BCI) design is mapping from population activity to BCI actuation.
  • This paper proposes using optimal control theory to formulate and improve BCI usability.
  • Main algorithmic proposals for mapping population activity to behavior:
    1. linear estimators
    2. Kalman filters
    3. Particle filters
    4. Neural net decoders
    5. point process filters
    6. kernel based techniques.
  • That is a lot of potential approaches. The nuances of the application would be required in order to sort them out.
  • MLE approach to BCI
    • Velocity kalman filter defined as: $\mathbf{y_t} = B\mathbf{v_t}^* + \mathbf{\epsilon_t }$ where $\mathbf{y_t}$ are $n$ neuron’s firing rates and $\mathbf{v_t}$ is the velocity of a prosethetic effector.
      • This is clear mathematically but I don’t know what a prosthetic effector is.
      • It seems like some implant that would drive neuron firing rates.
    • A second assumption is that this velocity changes smoothly over time.
    • Using these two assumptions: BCI control reduces to Bayesian inference over how this velocity results in firing rates.
      • I thought there would be more here since after this level of inference you’d still have to infer the previous problem of spike activity mapping to actions.
    • Using the above equations and the a posteriori estimate of $p(\mathbf{v_t} \mid y_1 … y_t)$, one can create a time dependent state update rule for a BCI controlled cursor position $\mathbf{p_t}$ using $\mathbf{v_t}$.
      • notation here is confusing because I thought y was in $\mathbb{R}^n$ as a firing frequency for n neurons. I take it the authors mean to use the 1 - t as $y$ at some previous recording time t.
      • This also answered my previous point about mpaping from $\mathbf{v_t}$ to actual actions.
    • While estimation based decoder control has remarkable progress in enabling cursor speed w/ in a factor of 2 of a natural limb, there are still some aspects that can be improved:
      1. Only decoders that correspond to simple physical systems work well.
      2. Estimation framework assumes static tuning but performance in closed-loop systems over time is often very different and offline decoders may not work well in long term.
      3. Biomemtic decoders are not guaranteed optimal. Translating signals in terms of basic human motor movements are not necessairly the best way to solve control problems.
    • Authors make 3 assumptions about the brain as optimal controller:
      1. The brain is emitting control signals that minimize some cost function.
      2. Primary cortex activity is a direct representation of these signals.
      3. End goal result of learning is to produce the optimal control signals of a given effector.
        • These assumptions have helped me understand a lot of what the paper is previously trying to build to.
        • Mainly, what I see now that I did not before is why the signal estimation approach is limiting and why understanding motor cotrex signals as effector signals is so important. I believe this is because control theory allows a framework for much more specific definitions of control when the goal is reconstructing effector signals instead of predicting movement. Predicting movement is often a more vague problem for a decoder while fine-grained analysis of how brain signals enable optimal control in reaching for example is much more specific. 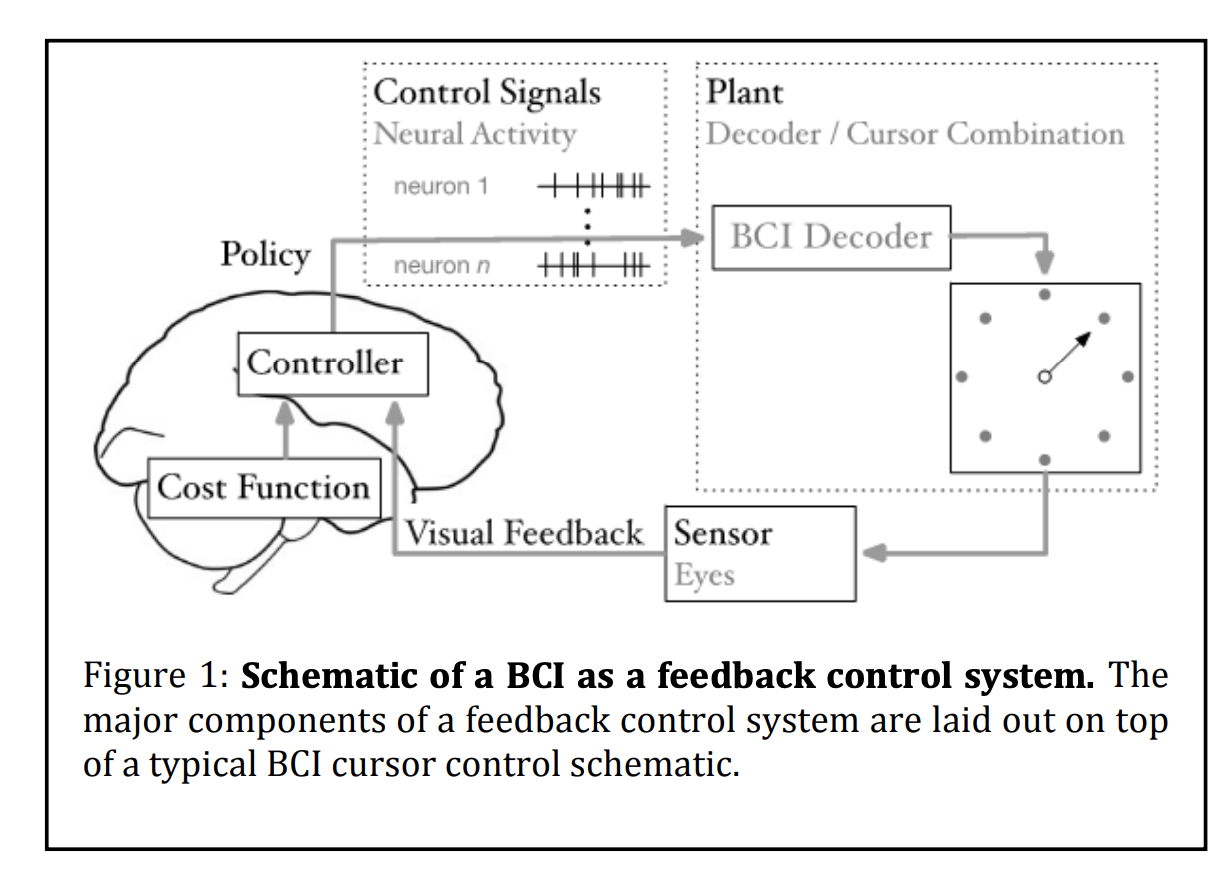bci schematic
    • I really like this figure since it is a straightforward diagram of the control model here.
    • It shows where that control signals feed into the plant for state updates in decoder.
    • $x$ as cursor state, $u$ as control signal, and $J(u)$ as cost function for signal $u$.
    • Optimal cost is $J^* = J^(u^*)$, plant parameters are $\phi$
    • $\phi$ determines the usefulness of BCI based on how it minimizes cost function.
    • Not so sure what $H_p$ and $H_v$ mean as spring like properties of the plant and viscous properties. Are these from control theory?
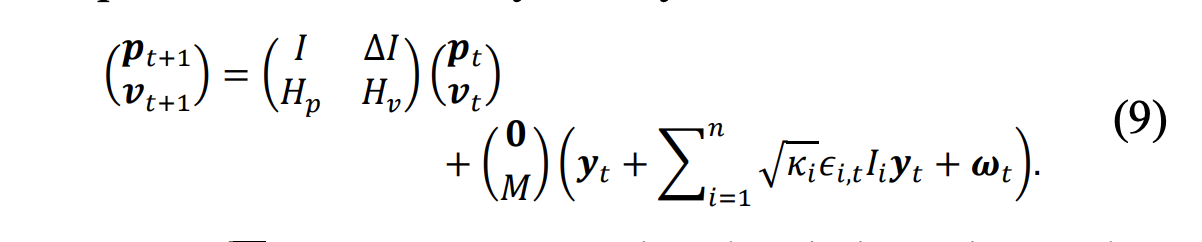
    • BCI plant system dyanmics bci schematic
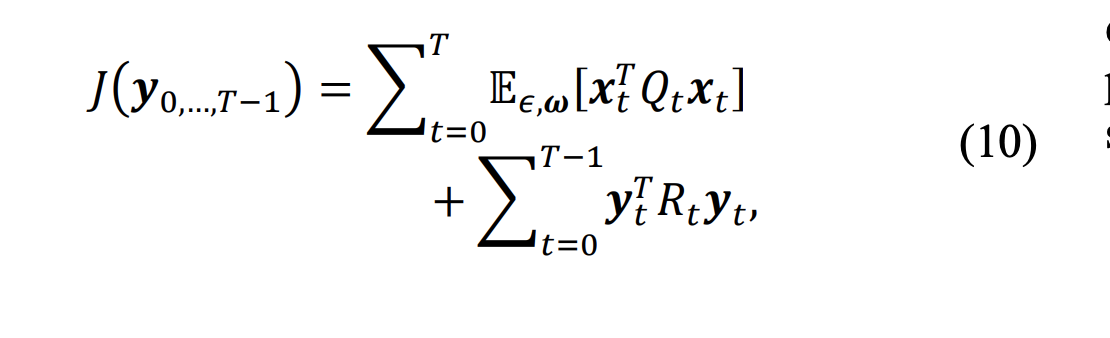
    • Quadratic cost function used in motor learning studies bci schematic
    • Normally I like to use latex to write out he equations in the paper but I don’t wan’t to the \bmatrix formatting today.
    • First solve forward control problem of optimizing $H_p$ and $H_t$.
    • Linear quadratic regulator gives minmial cost under optimal policy: $J*(H_p,H_t) = tr(P_0,X_0)$.
      • are $H_p$ and $H_t$ suppoed to be $H_p^$ and $H_t^$, the optimal conditions in order to get J*?

        Zhang 2016 on simulation results for this paper:

        In one sense, these results might seem trivial: the optimal 2D linear BCI plant is an integrator that provides no resistance on the inputs. This is an intuitive solution given that we assumed no bias in the control signals and further assumed a minimal effort constraint. In another sense, the results are quite surprising: the optimal dynamics identified through this approach to BCI design are qualitatively different from those of the typical BCI decoder, the VKF. In fact, the parameters identified with our method fall outside of the allowable parameters of a VKF.