Back to research

Multitask Learning For Cancer (MTL4C)

• See the code on github HERE
• See the technical report HERE
• “The aim of this report is to draw from adaptations and state of the art developments in both algorithms for recommender systems and multitask learning to model the interaction between cancer cell lines and cancer drugs.”
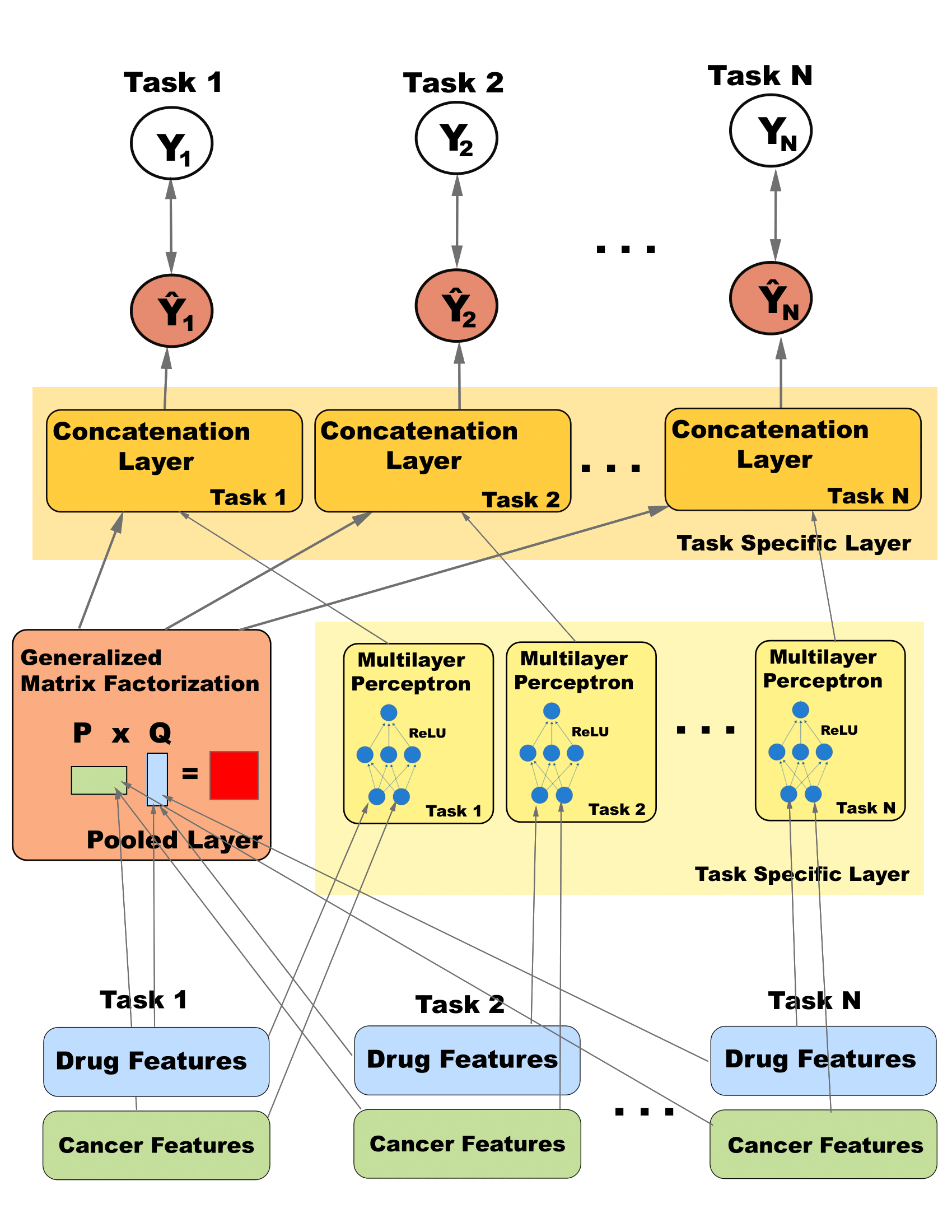
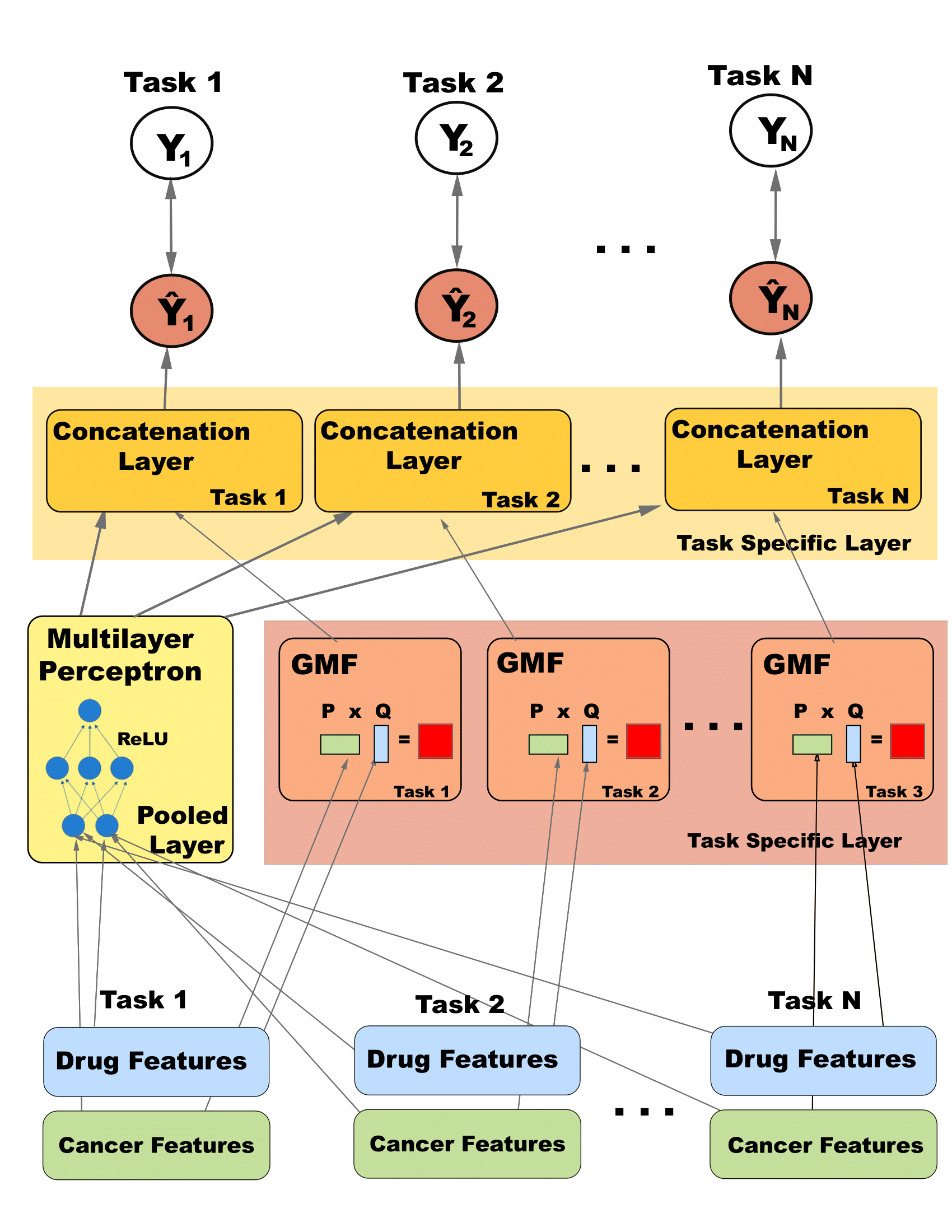
• Here is my adaptation of NCF
• Instead of using embeddings of row and column vectors $y_i^T$ and $y_j$ to represent feature data, our method uses Dragon7 drug features and Lincs cell line feature matrices for $U$ and $V$ to predict $Y$. In order to perform general matrix factorization, latent drug features $P$ and latent cell features $Q$ are learned as biased rank-d linear combinations of $U$ and $V$. \begin{equation} min_{P,Q}\; ||Y - P^TQ||_F \ \text{where} \ P = \boldsymbol{w}_vV + \boldsymbol{b}_v \ , \ Q = \boldsymbol{w}_uU + \boldsymbol{b}_u, \ \boldsymbol{w}_v, \boldsymbol{w}_u \in \mathbb{R}^d \end{equation}
• We adapted the method from classification to regression. The NCF paper presents likelihood function: \begin{equation} p(Y,Y^- \mid U,V, \Theta) = \prod\limits_{(i,j) \in Y}\hat y_{i,j} \prod\limits_{(i,j) \in Y^-}(1 -\hat y_{i,j}) \end{equation} Where $Y$ is a positive rating $Y^- $ is a negative rating. Taking the log and simplifying gives us the objective function used in NCF: \begin{equation} -\sum\limits_{(i,j) \in Y, Y^-} y_{i,j} \log(\hat y_{i,j}) + (1-\hat y_{i,j}) \log(1- y_{i,j}) \end{equation} In our method we are reconstructing a non binary ratings matrix $Y$ using a regression model. The likelihood function becomes: \begin{equation} p(Y \mid U,V, \Theta) = \prod\limits_{(y_{i,j}) \in Y}p(y_{ij} \mid \boldsymbol{u}_i, \boldsymbol{v}_j, \Theta) \end{equation}
  as the likelihood function, which is equal to minimizing the objective function

\begin{equation} \min_{U,V}\sum\limits_{y_{i,j} \neq 0 \in Y}(y_{i,j} - \boldsymbol{u}_i^T \boldsymbol{v}_j)^2 + \lambda_U ||\boldsymbol{u}_i||_{F} + \lambda_V ||\boldsymbol{v}_j||_{F}. \end{equation}

• Though the objective function has been adapted from classification to regression, we are still using the same process of neural collaborative filtering, which replaces the term $ U^TV = Y $ from Eq. 5 with $\sigma(\boldsymbol{h}^T \begin{bmatrix}\phi^{GMF} \\ \phi^{MLP}\end{bmatrix})$ where the large parenthesis denote concatenation, $\boldsymbol{h}^T$ are regularizing weights, $\phi^{GMF}$ is the function described in Eq. 1, and $\phi^{MLP} = a_L (W_L^T(a_{L-1}(…a_{1}(W_{1} \begin{pmatrix}U^T \\ V \end{pmatrix} + \boldsymbol{b}_1)…) + \boldsymbol{b}_{L-1}) + \boldsymbol{b}_L)$. The only difference is the final $\sigma$ is not sigmoid but linear activation. The $a$ values denote activation layers.

• Here is a flow chart for the adapted algorithm. Note the pooled layers for multitask.